• Imprimir
• Correo electrónico

La escuela Pitagórica

PITAGORAS (siglo VI a. de C.)

Filósofo griego, nacido probablemente en Samos, que, tras viajar por diversos países, se estableció en Crotona (Magna Grecia), donde fundó una comunidad integrada principalmente por aristócratas. Se le atribuye el famoso teorema de Pitágoras: La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Los pitagóricos descubrieron la relación matemática de la Escala musical, creían que los cuerpos celestes estaban a distancias armónicas, de tal manera que en su movimiento producían una especie de sinfonía: la famosa armonía de las esferas. Sus principios éticos se basaron en el ascetismo y produjeron hombres notables como Arquitas y Pitias.

Obras:

No ha llegado hasta nosotros ninguno de sus escritos. Conocemos su doctrina por sus discípulos y por referencias de autores posteriores.

LA ESCUELA PITAGORICA: LAS COSAS SON NÚMEROS

Todos los fenómenos físicos se pueden expresar matemáticamente. ¿Qué piensa al respecto? ¿Se llegará algún día a la expresión matemática del fenómeno de la vida?

Antes de entrar a desarrollar el tema de esta lectura, profundizaremos un poco más sobre el concepto de historia, sirviéndonos para esto del concepto de vida y de evolución.

Como objeto de reflexión consideremos un árbol en edad adulta. Su altura, su frondosidad, el grosor de su tallo, la forma de sus ramas, el color de sus hojas, etc., son el resultado de cuarenta, cincuenta o más años de lluvias, sequías, vendavales, cambios de temperatura, características del suelo, etc. Bajo condiciones distintas su estado actual habría sido otro, más bajo, menos frondoso, quizás se hubiera secado. Lo que el árbol es en este momento es el compendio de un pasado, de una historia. Esta historia va más allá de los cuarenta o cincuenta años, la semilla de la cual brotó tiene también un pasado que se remonta a millones de años. El árbol que observamos comenzó probablemente bajo la forma de un helecho gigante y éste bajo la forma de liquen o de musgo. ¿Y el musgo? No apareció de un momento a otro, tiene a su vez un pasado que llega hasta los comienzos de la vida misma, bajo la forma de las primeras moléculas orgánicas. Llegamos así al origen de la vida, sin embargo, aún estamos lejos del primer instante, a partir del cual comenzó, por decirlo así, a escribirse la historia del árbol, objeto de nuestra reflexión. La vida no comenzó de una manera súbita, sin preparación alguna en la materia inorgánica, ella tiene un pasado que nos lleva en la imaginación al comienzo mismo de la materia y del tiempo. Hasta ahora sólo hemos considerado una dirección en la historia, el pasado. El árbol tiene también futuro, comenzará a envejecer, se secarán sus raíces, se caerán sus hojas y terminará por servir de abono a nuevos retoños, de sus semillas surgirán nuevos árboles que prolongarán en el tiempo su propia historia.

Si en lugar del objeto anterior me tomo a mí mismo como ejemplo y pregunto, qué soy yo en este preciso momento, debería responder de una manera semejante: soy compendio y resultado de una larga cadena de acontecimientos que fueron tejiendo lo que constituye mi historia: yo soy historia y hago historia, mi vida no es un acontecimiento aislado, soy deudor del pasado y contribuyo, quiera o no, al futuro propio, y al de los demás.

Lo que hemos dicho de los individuos, debemos decirlo también de las creaciones de estos mismos individuos. Nuestros conocimientos actuales de matemáticas y de física no surgieron de un momento a otro en la mente de un hombre privilegiado, son el resultado de miles de condiciones, de miles de circunstancias, a lo largo de muchísimos años de historia. Las matemáticas, como cualquier otra creación del espíritu humano, tiene una historia. Comenzó en forma muy rudimentaria, unos descubrimientos servían de base a otros, se complementaban, se corregían hasta llegar al alto grado de perfección de nuestros días. Primero fue la aritmética, luego el álgebra, luego el cálculo y así sucesivamente; pero la historia no se detiene, y seguimos avanzando, nuestros conocimientos sirven de base a nuevos descubrimientos.

Antes de los griegos, los caldeos y los egipcios habían hecho importantes descubrimientos en la aritmética y en la geometría; sin embargo, son los griegos quienes por primera vez se dedican al estudio de estas materias de una manera desinteresada. Ya no se trata de resolver solamente problemas concretos de cálculo y de medición, se trata de investigar el misterio de los números y del espacio geométrico; es el comienzo de las matemáticas como ciencia, o mejor, como filosofía, es decir, como ocupación del espíritu, por amor a la especulación como tal, y no por su sola aplicación instrumental al mundo de la medida y del cálculo.

La escuela pitagórica debe su nombre a Pitágoras. Es muy poco lo que podemos saber acerca de este personaje, quizás no existió realmente. La tradición nos dice que nació hacia el año 580 antes de Cristo, se le atribuye, entre muchísimas otras cosas, el descubrimiento del famosísimo Teorema de Pitágoras: la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos. Aristóteles nos dice que fue el primero en ocuparse de matemáticas y de números.

La escuela pitagórica fue en sus comienzos una secta, en la que se mezclaban curiosamente la religión y la ciencia. Creían en la inmortalidad, en la transmigración de las almas, en la salvación individual a través del cultivo de la ciencia, en particular de la ciencia de los números. Se trataba de una especie de comunidad religiosa, dedicada a la meditación sobre los números, sus leyes y misterios. Todo esto nos puede parecer un tanto extraño, pero no olvidemos que estamos en los comienzos de las matemáticas, y los descubrimientos de los números y sus relaciones constituían algo así como una revelación. Han pasado muchos años, nuestros conocimientos superan notablemente a los de los primeros matemáticos, sin embargo, todos los días se escribe algo nuevo sobre los números y sus misteriosas combinaciones... «Ia magia de los números», «paradojas matemáticas», «el misterio de los números», etc.

¿No es algo supremamente curioso que la suma de los primeros cuatro números sea precisamente diez y que diez sea la base de toda la numeración decimal? ¿Cómo explicar la existencia de números que sólo son divisibles por sí mismos? (Números primos) ¿Y la sucesión de números pares e impares? El 1 es «impar», el 2 par, el 3 impar, el 4 par, el 5 impar, el 6 par y así sucesivamente.

La gran revelación para la escuela pitagórica fue el descubrimiento de que a cada número correspondía una figura y, por consiguiente, a cada figura un número. Ahora bien, todas las cosas tienen una figura, por lo tanto tienen un número que las define, que las hace tal cosa y no otra: las cosas son números.

Para nosotros los números son símbolos, el tres es simplemente 3, el cuatro, 4; para los griegos, en el tiempo de los pitagóricos, el 3 era un triángulo, el 4, un cuadrado, el 30, un rectángulo, etc., a cada número correspondía una figura. Intentemos explicarlo de la siguiente manera, comenzando con la unidad representada por un punto:

Los números triangulares son los siguientes:

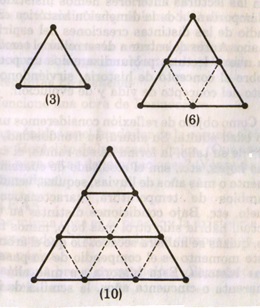
Los números cuadrados:

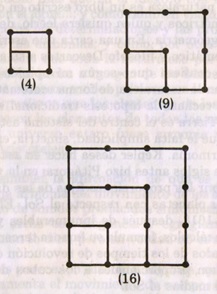
Los números rectangulares u oblongos:

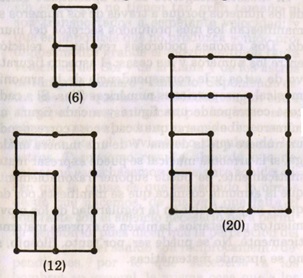
Los números pentagonales:

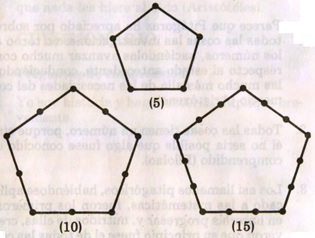
Aunque no es nuestro intento exponer de una manera detallada la teoría de los números de la escuela pitagórica, vamos a mostrar con un ejemplo cómo la aritmética «figurativa» lleva a conclusiones geométricas, por esta razón se la llama aritmogeometría. Si añadimos la figura que corresponde al cuadrado (9) a la figura que corresponde al cuadro (16) obtenemos un tercer cuadrado (25), uno de cuyos lados corresponde a la hipotenusa de un triángulo rectángulo cuyos dos catetos son (3) y (4) respectivamente; tenemos así la solución, en un caso concreto, al Teorema de Pitágoras:

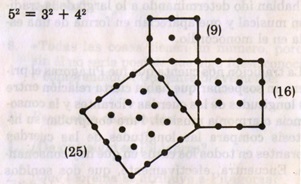
La suma de los cuadrados construidos sobre los catetos es igual al cuadrado construido sobre la hipotenusa; en este caso concreto, un triángulo rectángulo, cuyos catetos son (3) y (4), tiene una hipotenusa (5). Hoy en día expresamos lo mismo de la siguiente manera: 32 + 42 = 52; como este caso hay varios, en los cuales la suma de dos números cuadrados da un tercer número cuadrado, uno de cuyos lados corresponde exactamente a la hipotenusa del triángulo formado por los lados de los otros dos cuadrados: por ejemplo: la figura cuadrada que corresponde al número 25, añadida a la figura cuadrada que corresponde al número 144, nos da una tercera figura cuadrada que corresponde al número 169, o sea: 52 + 122 = 132; el triángulo formado por las tres figuras tiene de lados (5) y (12) Y de hipotenusa (13).

Otro gran descubrimiento viene a corroborar la tesis pitagórica de que las cosas son números, el descubrimiento de que la armonía musical sigue ciertas leyes numéricas. Si se hace vibrar una cuerda tensa sobre una caja de resonancia se obtiene una nota, si se divide la longitud de la cuerda por medio de un soporte o puente, se pueden obtener notas diferentes en cada uno de los segmentos en que se divide la cuerda. Este instrumento musical constituye el monocordio, conocido desde la más remota antigüedad y que los griegos recibieron de los egipcios. El tono de la nota producida por el monocordio depende de la longitud de la cuerda vibrante, más bajo cuanto más larga, y más alto cuanto más corta. La música no es más que la combinación sucesiva de diferentes sonidos o notas que produce una sensación agradable al oído. Ahora bien, hay un primer hecho musical aceptado universalmente: sólo algunas combinaciones de dos notas, son agradables al oído, es decir consonantes. Las otras combinaciones de dos notas, son disonantes. La armonía, por lo tanto, es una condición impuesta al músico. Esta condición se manifiesta concretamente en las posiciones permitidas al puente, que se habían ido determinando a lo largo de la tradición musical y que aparecían en forma de una escala en el monocordio.

La tradición nos cuenta que fue Pitágoras el primero en sospechar que había cierta relación entre las longitudes de las cuerdas vibrantes y la consonancia o armonía musical. Para comprobar su hipótesis compara las longitudes de las cuerdas vibrantes en todos los casos en que hay consonancia. Encuentra, efectivamente, que dos sonidos son consonantes cuando las respectivas longitudes son entre sí como 1 a 2; o como 2 a 3; o como 3 a 4. Si por el contrario, las longitudes no cumplen con estas proporciones, el resultado es una disonancia, y en este caso se trata de un ruido, y no, de música. Por primera vez en la historia de la música se encuentra que la armonía se puede expresar matemáticamente: dos notas consecutivas son consonantes, suenan bien, si las longitudes de los segmentos de la cuerda vibrante en el monocordio son como los números enteros sencillos, como 1 a .2; como 2 a 3, como 3 a 4; en caso contrario, son disonantes.

La importancia de este descubrimiento fue enorme. La música desempeñaba un papel de primer orden dentro de la educación y de la cultura griega. Si la música está sometida a leyes numéricas, ¿por qué no, la astronomía, y con la astronomía, el universo entero? ¿No se puede pensar, acaso, por analogía con la música, que las distancias de los planetas guardan entre sí cierta proporción fija de acuerdo con una especie de armonía cósmica, de tal manera que produjeran en la inmensidad del espacio una sinfonía perenne?

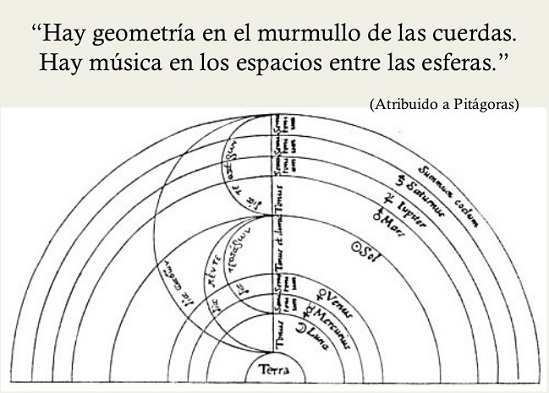
La escuela pitagórica desapareció casi por completo hacia el siglo III antes de Cristo, entre otras razones, por la inmensa autoridad de Platón y de Aristóteles quienes la atacaron acérrimamente, en especial éste último. Sin embargo, su programa y su espíritu reapareció nuevamente en Occidente, durante la Edad Media. Entre sus principales representantes se encuentran Copérnico, Kepler, Galileo y el mismo Descartes. Para Galileo la naturaleza es un libro escrito en caracteres geométricos y quien quisiera leerlo, debería aprender geometría. En una carta que escribe el gran matemático y filósofo Descartes a su amigo Mersenne confiesa que «según mi opinión todo acontece en la naturaleza de forma matemática».

Copérnico rechaza la hipótesis tradicional según la cual la Tierra es el centro del sistema astronómico porque le falta simplicidad, simetría, en una palabra, armonía. Kepler desea hacer en astronomía lo que siglos antes hizo Pitágoras en la música: descubrir las proporciones fijas de las distancias de los planetas con respecto al Sol. El 8 de marzo de 1618, después de innumerables y dispendiosos cálculos, formula su famosa tercera ley: los cuadrados de los tiempos de revolución de los planetas son proporcionales a los cubos de sus distancias medias al Sol.

El filósofo pitagórico es un apasionado cultor de los números porque a través de los números se manifiestan los más profundos secretos del mundo. Dos razones poderosas revelan la relación entre los números y las cosas: el aspecto figurativo de estos y la correspondencia de la armonía musical a proporciones numéricas fijas. Si a cada cosa corresponde una figura y a cada figura un número, cabe esperar que a cada cosa corresponda un número que la defina. Y de una manera análoga, si la armonía musical se puede expresar matemáticamente, se puede suponer razonablemente que la armonía cósmica que se manifiesta por doquier, en particular en la regularidad de los movimientos planetarios, también se expresa matemáticamente. No se puede ser, por tanto, filósofo, si no se aprende matemáticas.

TEXTOS

1. Parece que Pitágoras ha apreciado por sobre todas las cosas las investigaciones en torno a los números, haciéndolas avanzar mucho con respecto al estado antecedente, conduciéndolas mucho más allá de las necesidades del comercio (Aristóxeno).

2. Todas las cosas tienen un número, porque sin él no sería posible que algo fuese conocido o comprendido (Filolao).

3. Los así llamados pitagóricos, habiéndose aplicado a las matemáticas, fueron los primeros en hacerlas progresar y, nutridos de ellas, creyeron que su principio fuese el de todas las cosas..., y les pareció observar en los números semejanzas con los seres y con los fenómenos, mucho más que en el fuego o con la tierra o con el agua...; y como también veían en los números las determinaciones y las proporciones de las armonías; y como, por otra parte, les parecía que toda la naturaleza por lo demás estaba hecha a imagen de los números y que los números son los primeros en la naturaleza, supusieron que los elementos de los números fuesen los elementos de todos los seres y que el universo entero fuese armonía y número (Aristóteles).

4. También la afirmación de que se engendra una armonía del movimiento de los astros, como de sonidos producidos sinfónicamente, está dicho con elegancia y egregiamente por quien lo dice, pero en verdad no es así.

Les parece, en efecto, a algunos, que necesariamente el movimiento de cuerpos tan grandes debe producir un sonido, pues se produce también por los cuerpos entre nosotros, y que, sin embargo, no tienen tan gran tamaño ni son transportados a semejante velocidad; y que es imposible que no produzca sonido prodigiosamente grande el movimiento de tanta velocidad del Sol y de la Luna y de los astros de tan gran número y tamaño. Suponiendo estas cosas, y que las velocidades tengan entre sí proporciones sinfónicas, por los intervalos, afirman que se produce un sonido de acuerdo perfecto por el movimiento circular de los astros. Pero como resulta absurdo que nosotros no escuchásemos semejante sonido, dicen que la causa es que ese sonido lo oímos desde que nacemos, de manera que falta el contraste con el silencio necesario para permitir percibirlo, pues dicen que la percepción del silencio y la del sonido son recíprocamente dependientes, por lo que sucedería a los hombres en general, la misma cosa que a los forjadores, a quienes, por la costumbre parece que nada les hiere al oído (Aristóteles).

• Ant
• Siguiente